一文详解,PID控制中P、I、D参数调整策略与技巧

我们来详细探讨一下PID控制器中P（比例）、I（积分）、D（微分）三个参数的调整方法。PID控制是自动控制领域中最常用、最基础且有效的控制策略之一，其核心在于通过不断调整这三个参数，使系统的输出尽可能接近期望值（设定值）。
"一、 PID控制器简介"
PID控制器是一种线性、定常、无限脉冲响应（IIR）的控制器。它根据设定值（Setpoint）与实际输出值（Process Variable, PV）之间的误差（Error, E = Setpoint - PV），通过比例（P）、积分（I）、微分（D）三种运算，产生控制输出（Output），去驱动被控对象（Process），以减小误差。
"P (Proportional) 比例控制：" 控制作用与当前误差成正比。 "作用：" 提供主要的控制力，快速响应误差变化。 "效果：" 减小稳态误差，但可能导致超调和振荡。 "公式：" `P_term = Kp E(t)` "Kp (比例增益)：" 决定比例作用的强度。Kp越大，响应越快，超调可能越大；Kp越小，响应越慢，稳态误差可能越大。 "I (Integral) 积分控制：" 控制作用与

相关内容：

　　使用PID控制器对积分过程进行控制，首先要了解控制器比例（P）、积分（I）和微分（D）在控制积分过程中所起的作用。对积分过程进行PID控制，与自整定过程控制存在一定的相似之处，但在一些重要方面却有很大差异。

本文图片来源：CEChina.cn

　　如何调节PID控制器，取决于过程响应的类型。换言之，一旦将PID控制器与某一过程匹配，这对组合的行为方式便具有该（类）过程的特性。此外，PID/积分过程的表现方式以及相应的整定方法，与PID/自整定过程是不同的。关注点不同，规则也不同。

　　如同分析自整定过程一样，我们将从控制器比例、积分、微分各自对积分过程的影响入手，并借鉴自整定过程的分析方法，探索如何将三者结合以实现有效的控制器设计。

　　比例与积分过程的相互作用

　　这里有几件事情需要讨论，首先是积分过程的过程比例定义（见图 1）。在自整定过程中，过程比例（Kp）被定义为过程变量（PV）的变化量与控制器输出（OP）的变化量之比，用ΔPV/ΔOP来表示。但如果你改变连接到积分过程的控制器输出，假以时日，过程变量（PV）最终会趋向正无穷大（或负无穷大）。因此，自整定过程中关于过程比例的定义对于积分过程来说是没有用的，因为结果总是 “无穷大”。

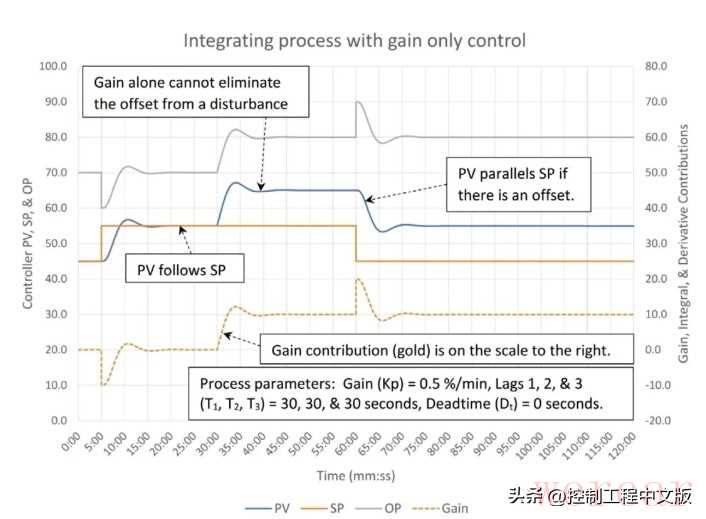
▲图1：仅采用比例（P）控制（控制器增益K=1.0）时，积分过程的响应情况。

　　我们真正需要知道的是，当我们改变控制器输出时，过程变量（PV）的变化量会是多少呢？这被定义为Kp= (ΔPV/分钟)/ΔOP{(%/分钟)/%}。为了简便起见，通常把积分过程的过程比例表示为 %/分钟，要清楚这是指控制器输出每变化1%时的情况（注意，干扰也用控制器输出变化的百分比来表示）。

　　当我们观察在5分钟时间点控制器设定值（SP）的变化情况，就会注意到过程变量无需积分作用，就能达到设定值。这与自整定过程截然不同，在自整定过程中，需要积分作用才能将过程变量驱动到设定值。这是怎么回事呢？

　　像液位这样的物料（或能量）平衡过程，会维持一个库存量，只要输入和输出流量速率相匹配，该库存量就不会改变。设定值的变化并不会改变不受控制的流量（输入或输出），它仅仅是一个改变库存量的指令。在这种情况下，控制器通过减少输出流量来实现这一点，直到库存量与设定值匹配为止。此时，当误差降为零时，比例作用也降为零，并且控制器输出会回到起始状态，此时物料平衡得以恢复。

　　对积分过程的整定策略

　　之所以强调这个看似微不足道的点，是因为它会显著影响如何看待对积分过程的整定（更重要的是，你必须忘掉控制器比例在自整定过程中是如何起作用的）。有一点需要注意，当你对积分过程的设定值进行调整时，积分作用实际上会适得其反。

　　在30分钟时间点入口流量增加了10%（相当于控制器输出的变化量）。为了匹配入口流量的变化，控制器输出必须增加10%。只有当过程变量与设定值之间的误差乘以控制器增益，等于入口流量的变化量时，才会出现这种情况，即{ΔOP=Δ入口流量=(PV–SP)*K}。就像自整定过程一样，对积分过程的干扰会导致过程变量与设定值之间产生永久性偏差，除非使用积分作用。最后，在60分钟时，设定值再次被更改。过程变量与设定值的变化保持同步，维持着30分钟时点入口流量变化所导致的恒定偏差。

　　从积分过程仅采用比例的控制中，我们了解到的是：

　　■ 过程变量将跟随设定值的变化，而无需积分作用。实际上，积分作用很可能会适得其反。

　　■ 干扰会导致过程变量与设定值之间产生持续的偏差。需要积分作用来消除这种偏差。

　　这给我们带来了一些在自整定过程中不会遇到的问题。

　　其一，如果必须在针对设定值变化的调节和抗干扰调节之间取得平衡，那么就面临一个平衡问题：我们可以加入多少积分作用来消除干扰，同时又不影响对设定值变化的响应呢？幸运的是，在积分过程中我们几乎从不更改设定值（至少在炼油厂是这样），所以这通常不是一个问题。

　　第二个问题是，我们不能通过更改设定值来测试控制器如何调节来应对干扰（见图 2）。

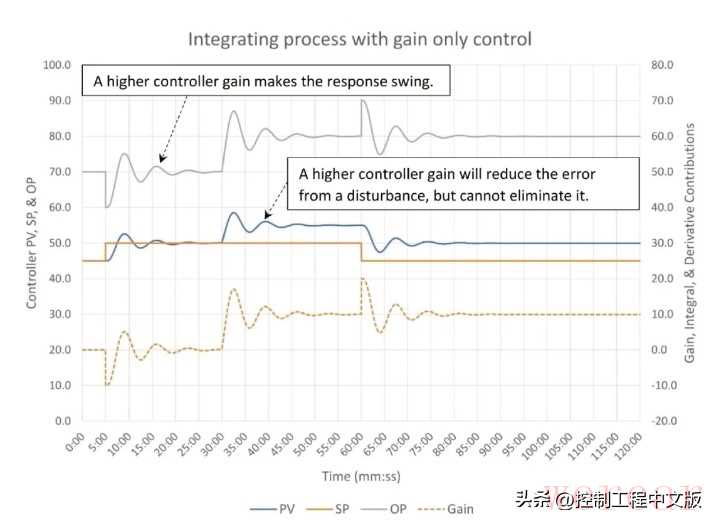
▲图2：仅采用比例控制（控制器比例K=2.0）时，积分过程的响应情况。

　　和图1一样，在图2中的30分钟时点，输入流量也变化了10%。经过初始振荡后，控制器输出变化10%，以匹配输入的变化。较高的控制器增益可以减小过程变量与设定值之间的偏差，然而，它无法也不能消除这种偏差。该表现与自整定过程的表现相同；提高控制器比例，会减小过程变量与设定值之间的偏差，但存在增加控制器振荡的风险（见图3）。

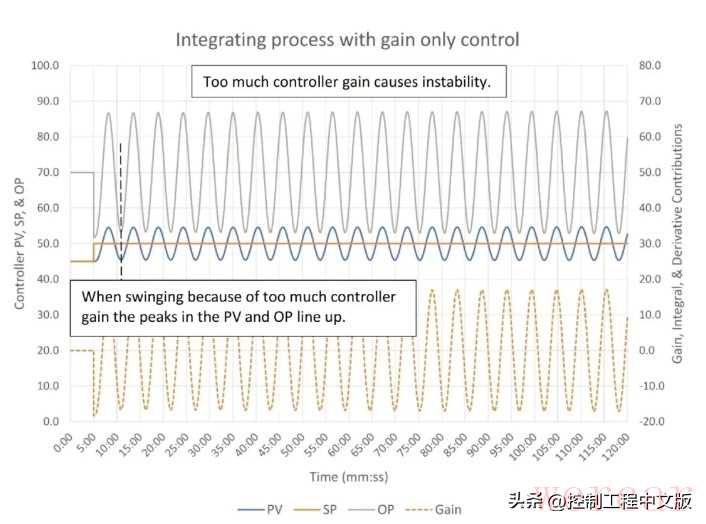
▲图3：仅采用比例控制（控制器比例K=3.65）时，积分过程的响应情况。

　　图3表明，与自整定过程类似，如果控制器比例过高，控制器就会变得不稳定。此外，过程变量和控制器输出的峰值会接近，在启发式控制器整定过程中，这是可利用的一个关键视觉线索。

　　积分与积分过程的相互作用

　　图4表明，仅采用积分控制对积分过程是行不通的。积分过程的一个特点是，无论积分调节常数（Ti）设置得多么小，仅靠积分控制总是不稳定的。在积分过程中，一个常见的调节问题是，相对于积分调节常数而言，控制器比例不足，这会导致过程持续缓慢地变化。(图4使用并行PID算法，以展示在没有控制器比例时，积分作用是如何不起作用的。）

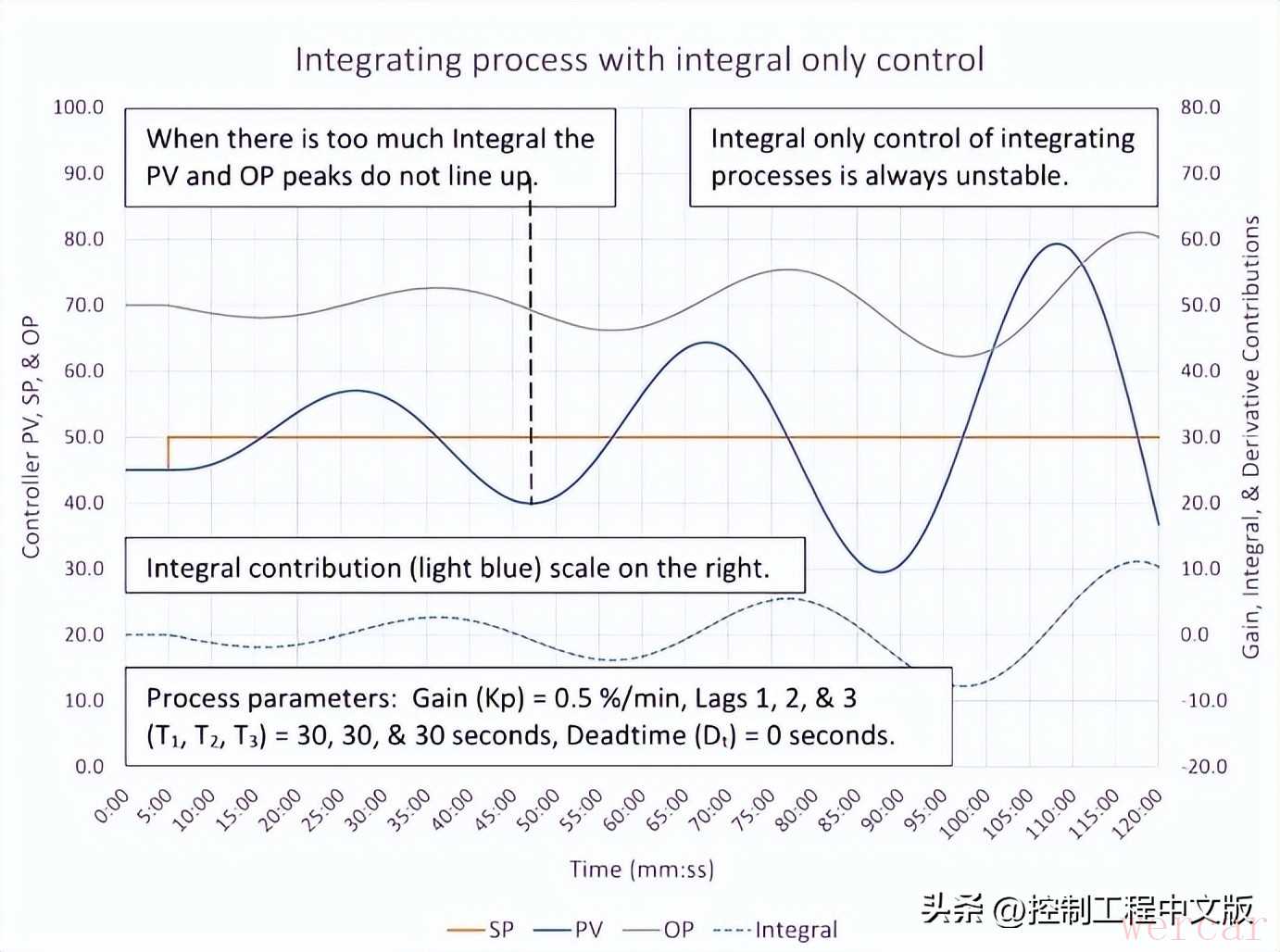
▲图4：仅采用积分（I）控制（积分Ti=0.05 次/分钟，并行PID算法）时，积分过程的响应情况。

　　与自整定过程类似，当积分作用过强（相对于控制器比例而言）时，过程变量和控制器输出的峰值不会接近。图5展示了在积分过程的积分控制（PI控制）中，加入控制器比例后会发生什么情况。

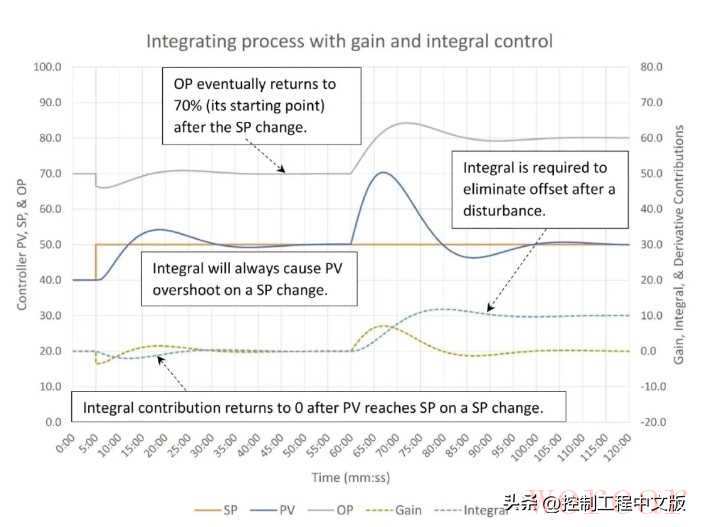
▲图5：积分过程的PI控制（K=0.35，Ti=0.05 次/分钟，并行PID算法）。

　　从图5中我们可以看到，在控制器中加入控制器比例可以使控制器稳定下来，同时保持积分常数为0.05次/分钟（并行PID算法）。在5分钟时点，对设定值变化的响应仍有一点波动；进一步提高控制器比例可以消除这种波动。请注意，在5到12分钟之间，积分作用使控制器输出恢复到70% 的速度变慢。这会导致过程变量超过了设定值（当存在积分时，在设定值变化后，过程变量总是会超过设定值）；随着积分贡献变为零，又过了20分钟过程变量才回到设定值。简而言之，积分的存在阻碍了控制器对设定值变化的响应。

　　在60分钟时点，对干扰的响应与自整定过程的响应相同。正如预期的那样，控制器比例首先做出响应，随后积分作用试图消除偏差。在经过一些波动后，随着过程变量稳定在设定值上（误差已恢复为零），控制器比例的作用降为零，并且积分作用（以及控制器输出的变化量）与干扰的大小相匹配（10%）。

　　这说明了积分过程整定中的一个问题；积分对于消除由过程干扰引起的过程变量偏差是必需的，但它会阻碍控制器对设定值变化的响应。幸运的是，在大多数积分过程中，很少更改设定值。

　　微分与积分过程的相互作用

　　图6展示了微分是如何抑制过程变量变化的。从30分钟时点开始，入口流量4%的扰动导致过程变量以每分钟2%的速率上升。4分钟的微分常数，使控制器输出产生足够的变化，从而将上升速率降低到每分钟 0.67%。（使用60秒的微分滤波器，是为了使微分响应足够慢，以便你能看到微分的影响。请注意，很少有控制系统允许给微分添加滤波器。）针对过程变量变化的微分作用（这是微分控制的推荐选项），对5分钟时点设定值的变化没有响应。

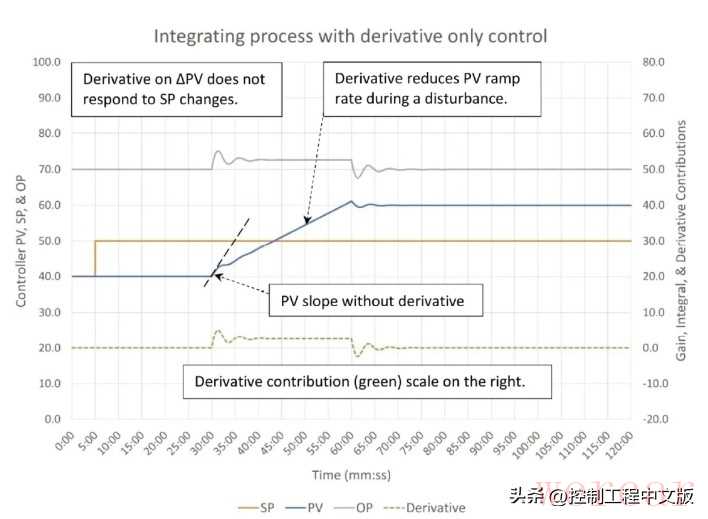
▲图6：仅采用微分（D）控制（微分时间Td=4分钟，微分滤波器时间=60秒，并行 PID 算法）时，积分过程的响应情况。

　　图7展示了增大微分作用是如何影响控制器性能的。微分作用过强会导致控制器振荡。进一步增大微分作用，将导致控制器不稳定。与自整定过程类似，微分作用过强的表现是：由于强微分作用追踪过程变量变化速率的微小变化，导致控制器输出快速波动。请注意，增大微分作用确实进一步降低了过程变量的变化速率。

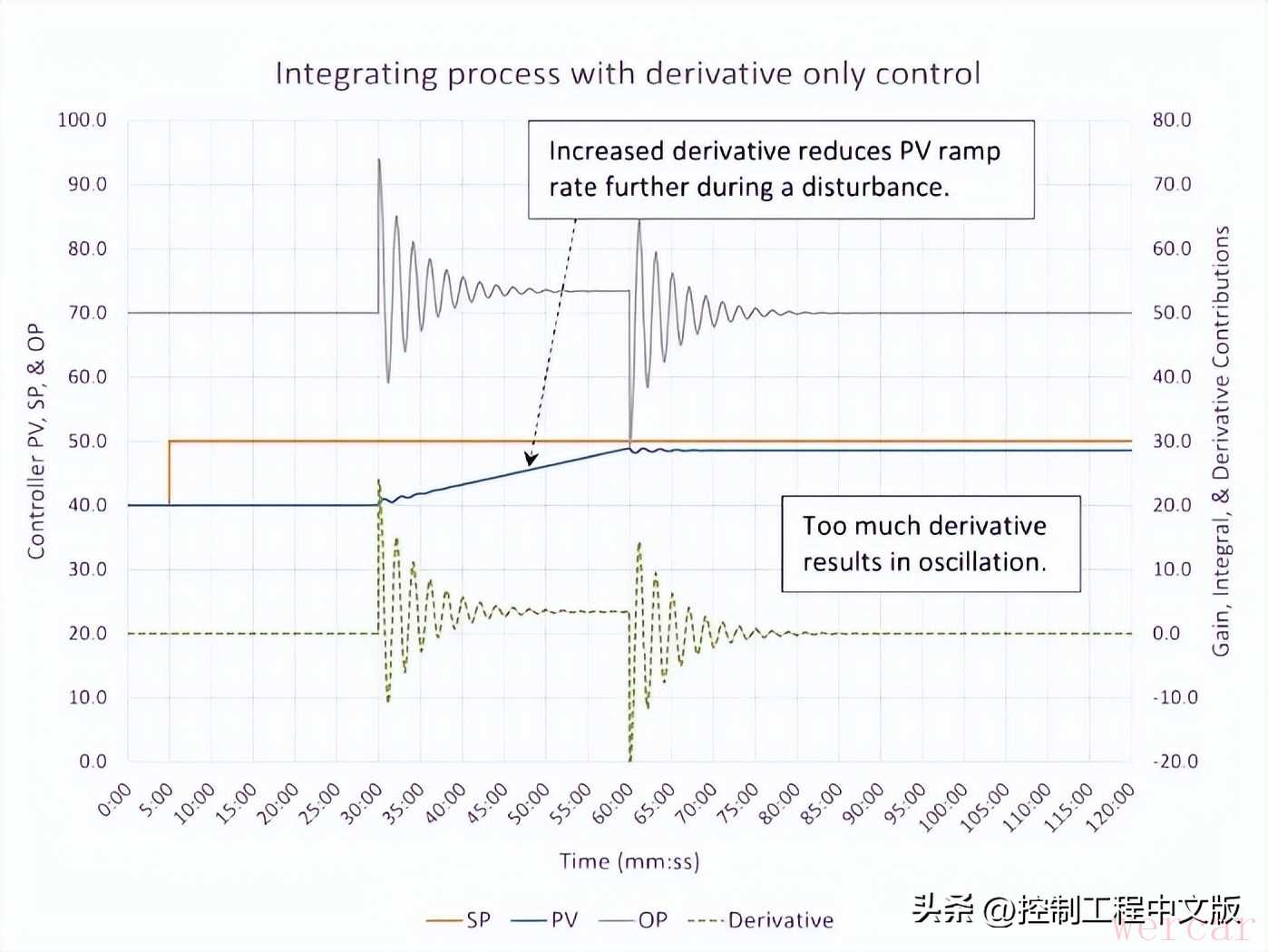
▲图7：仅采用微分（D）控制（微分时间Td=12分钟，微分滤波器时间=0秒，并行PID算法）时，积分过程的响应情况。

　　一般来说，微分从不用于液位控制。微分作用会使入口流量的微小变化导致出口流量产生较大变化，这会扰乱下游的工艺过程。液位控制通常会进行调节，无论入口流量如何变化，都不会导致出口流量出现快速变化，从而抑制任何干扰。这种流量波动管理，需要特别关注控制器的调节，以避免容器溢出或排空，同时还要尽量减少对下游工艺过程流量变化的影响。当然，这一规则也有例外情况，取决于具体的工艺过程和要求。

　　对积分过程进行PID控制与自整定过程控制的异同

　　我们已经了解到，积分过程对PID控制的响应在某些方面与自整定过程相似，而在另一些方面则有很大差异。

　　相似之处包括：

　　■ 控制器比例无法消除由过程干扰引起的过程变量与设定值之间的误差。需要积分作用来消除该误差。

　　■ 控制器比例过高会导致振荡。控制器比例过高表现为过程变量和控制器输出的峰值会一致。

　　■ 积分作用过强会导致振荡。积分作用过强表现为过程变量和控制器输出的峰值不一致。

　　■ 微分作用过强会导致振荡。

　　不同之处在于：

　　■ 控制器比例就足以应对设定值的变化。过程变量无需积分作用，就能回到设定值。实际上，积分会导致过程变量超过设定值，并延迟过程变量最终回到设定值所需的时间。

　　■ 在积分过程中，仅靠积分总是不稳定的。需要控制器比例来维持稳定控制。看似积分作用过强，实际上可能是控制器比例过小（启发式调节不像仅仅减慢积分作用那么简单）。

　　■ 微分通过抑制过程变量的变化，减缓由干扰引起的上升速率。

　　与自整定过程一样，良好的控制回路整定意味着将控制器比例、积分以及微分（很少情况下用到的）融合在一起，以获得“最佳”的控制器响应。其中一个挑战是“最佳”的定义，因为目标之一是避免对下游工艺过程造成不必要的干扰。我们会发现，积分过程的整定思路既有与自整定过程相似之处，也存在显著差异。

　　关键概念：

　　■ 了解仅靠积分作用，总会导致系统不稳定。当出现振荡时，过程变量和输出的峰值不会靠近。

　　■ 探究仅靠微分作用，将如何减缓过程变量的变化速率。微分作用过强，会导致系统不稳定。

　　思考一下：

　　当积分过程由PID控制器控制时，其表现与自整定过程有哪些相似和不同之处？